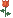مبرهنة فيثاغورسمبرهنة فيثاغورس هي مبرهنة في الهندسة الإقليدية، تقول أنه في أي مثلث قائم الزاوية يكون مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة يساوي مربع طول الوتر. سميت هذه المبرهنة على العالم فيثاغورس الذي كان رياضيا، و فيلسوفا، و عالم فلك في اليونان القديمة.
 الصيغة الهندسية لمبرهنة فيثاغورسالمبرهنةمبرهنة فيثاغورس المباشرة
الصيغة الهندسية لمبرهنة فيثاغورسالمبرهنةمبرهنة فيثاغورس المباشرةوهي الشكل الأكثر شهرة لمبرهنة فيثاغورس:
« في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة. »
في مثلث ABC قائم الزاوية في C، أي أن [AB] هو الوتر، نضع AB=c و AC=b و BC=a. لدينا:



تمكن مبرهنة فيثاغورس من حساب طول أحد أضلاع مثلث قائم الزاوية بمعرفة طولي الضلعين الآخرين. مثلا: إذا كان b=3 و a=4 فإن

ومنه

مثلوث ثلاثة أعداد صحيحة تمثل أطوال أضلاع مثلث قائم الزاوية، مثل (5 ،4 ،3)، يسمى مثلوث فيثاغورس.
مبرهنة فيثاغورس العكسيةنص مبرهنة فيثاغورس العكسية (العبارة 47 من الجزء الأول من كتاب العناصر لإقليدس):
« في مثلث، إذا كان مربع طول أطول ضلع يساوي مجموع مربعي طولي الضلعين الآخرين، فإن هذا المثلث قائم الزاوية. الزاوية القائمة هي الزاوية المقابلة لأطول ضلع، و الضلع الأطول هو الوتر. »
مبرهنة فيثاغورس هي خاصية مميزة للمثلث القائم الزاوية. بتعبير آخر:
« في مثلث ABC، إذا كان AC²+BC²=AB² فإن هذا المثلث قائم الزاوية في C .»
تاريخ المبرهنةعرفت خاصية فيثاغورس في العصور القديمة، والدلائل على ذلك ما زالت موجودة إلى الآن. يكفي مثلا أن نلاحظ الحبل ذا ثلاث عشرة عقدة الذي كان المسّاحون المصريون يستعملونه والذي نجد له صورا في عدة تصاوير للأعمال الزراعية. يسمح هذا الحبل، علاوة على قياس المسافات، بإنشاء زوايا قائمة دون الحاجة إلى جيب التمام، إذ تسمح العقد الثلاث عشرة (والمسافات الاثنتي عشرة الفاصلة بين العقد) من إنشاء مثلث أبعاده (5 ،4 ،3)، مثلث يتضح أنه قائم الزاوية. ظل هذا الحبل أداة هندسية طيلة العصور الوسطى.
أقدم تمثيل لمثلوثات فيثاغورس (مثلث قائم الزاوية وأطوال أضلاعه أعداد صحيحة طبيعية) نجده في الميغاليثات (2500 سنة قبل الميلاد). كما أظهرت آثار البابليين (لوحة Plimpton، حوالي سنة 1800 قبل الميلاد) أنه قبل ظهور فيثاغورس بأكثر من 1000 سنة، عرف المهندسون وجود مثلوثات فيثاغورس.
لكن بين اكتشاف الخاصية «نلاحظ أن بعض المثلثات القائمة الزاوية تحقق هذه الخاصية»، تعميمها «يبدو أن كل المثلثات القائمة الزاوية تحقق هذه الخاصية» وإثباتها «كل المثلثات القائمة الزاوية (فقط) في المستوى الإقليدي تحقق هذه الخاصية» عدة أجيال.
ندرة الدلائل التاريخية تجعلنا غير قادرين على نسب المبرهنة إلى فيثاغورس بشكل قاطع، مع أننا على يقين بأنه صاحبها. أول برهان مكتوب نجده في كتاب العناصر لإقليدس بالصيغة التالية:
« في المثلثات القائمة الزاوية، مربع طول الضلع المقابل للزاوية القائمة يساوي مجموع مربعي طولي الضلعين الآخرين. »
مع صيغتها العكسية: « إذا كان مربع طول ضلع في مثلث يساوي مجموع مربعي طولي الضلعين الآخرين، فإن الزاوية المحصورة بين هذين الضلعين قائمة. »
ومع ذلك، فتعليقات Proclus على كتاب العناصر لإقليدس (حوالي 400 سنة بعد الميلاد) تشير إلى أن إقليدس لم يقم سوى بإعادة تدوين برهان قديم نسبه Proclus إلى فيثاغورس.
إذن، يمكننا أن نؤرخ البرهان على هذه الخاصية ما بين القرن الثالث والقرن السادس قبل الميلاد. يحكى أنه في تلك الفترة اكتشفت الأعداد اللاجذرية. بالفعل، يمكن بسهولة إنشاء مثلث قائم الزاوية ومتساوي الساقين طول أحدهما 1، فيكون مربع طول الوتر هو 2. برهان بسيط أيام فيثاغورس يثبت أن العدد 2 ليس مربعا لعدد جذري. يقال أن هذا الاكتشاف تم إبقاؤه سرا من طرف المدرسة الفيثاغورسية تحت تهديد بالقتل.
إلى جانب هذه الاكتشافات، يبدو أن هذه المبرهنة عرفت في الصين أيضا. نجد إشارة إلى وجود هذه المبرهنة في واحد من أقدم المؤلفات الصينية في الرياضيات، كتاب Zhoubi suanjing. هذا المؤلف، كتب على الأغلب في Han Dynasty (أعظم الفترات في تاريخ الصين)، (206 قبل الميلاد، 220 سنة بعد الميلاد) يضم التقنيات المستعملة في فترة Zhou Dynasty. (القرن العاشر قبل الميلاد، 256 قبل الميلاد). نجد برهان هذه الخاصية، التي تحمل في الصين اسم مبرهنة جوجو Gougu (القاعدة والارتفاع)، في كتاب Jiuzhang suanshu (الفصول التسعة في فن الرياضيات، 100 سنة قبل الميلاد، 50 سنة بعده)، برهان مختلف كليا عن برهان إقليدس.
كما نجد في الهند برهانا عدديا للخاصية يعود إلى القرن الثالث قبل الميلاد (برهان باستعمال أعداد خاصة، لكن يمكن تعميمه بسهولة).
رغم أنها خاصية هندسية، إلا أنها أخذت منحى حسابيا عند البحث عن جميع مثلوثات أعداد صحيحة طبيعية تمثل أطوال أضلاع مثلث قائم الزاوية: أي مثلوثات فيثاغورس. هذا البحث فتح الباب لبحث آخر: البحث عن المثلوثات التي تحقق an + bn = cn، بحث قاد إلى مظنونة فيرما التي تم حلها سنة 1994 على يد الرياضي (بالإنكليزية: Andrew Wiles).
توجد في الحقيقة العديد من البراهين على هذه الخاصية، مثل برهان إقليدس، وبرهان الصينيين، مرورا ببرهان الهنود، وبرهان دا فينشي وحتى برهان الرئيس الأمريكي (بالإنكليزية: James Abram Garfield). كما لا يفوتنا ذكر الكاشي الذي عمم هذه المبرهنة على كل المثلثات: مبرهنة الكاشي.
 برهان بصري لمثلث أطوال أضلاعه (3، 4، 5) في كتاب Chou Pei Suan Ching (القرن الثاني-القرن الخامس قبل الميلاد)
برهان بصري لمثلث أطوال أضلاعه (3، 4، 5) في كتاب Chou Pei Suan Ching (القرن الثاني-القرن الخامس قبل الميلاد)